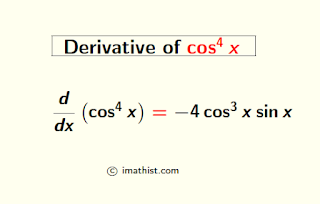The derivative of cos4(x) is equal to -4cos3(x) sinx. In this post, we will learn how to find the derivative of cos to the power 4 of x.
Derivative of cos4x Formula
The derivative of $\cos^4(x)$ is denoted by $\dfrac{d}{dx}(\cos^4 x)$ or $(\cos^4 x)’$. The formula of the derivative of cos^4(x) is given below:
$\dfrac{d}{dx}(\cos^4 x)=-4\cos^4 x \sin x$, or $(\cos^4 x)’=-4\cos^4 x \sin x$.
Derivative of cos4x
Question: What is the Derivative of $\cos^4x$?
Answer: The Derivative of $\cos^4x$ is $-4\cos^3 x \sin x$.
Proof:
Step 1: Let us assume that $z=\cos x$. Then we can write our function as
$\cos^4x=z^4$
Step 2: Note that $\dfrac{dz}{dx}=-\sin x$ as $z=\cos x$.
Step 3: By the chain rule, the derivative of $\cos^4x$ will be equal to
$\dfrac{d}{dx}(\cos^4x)=\dfrac{d}{dz}(z^4) \cdot \dfrac{dz}{dx}$
$=4z^3 \cdot (-\sin x)$ by the power rule of derivatives: $\dfrac{d}{dx}(x^n)=nx^{n-1}$
$=4\cos^3 x \cdot (-\sin x)$ as $z=\cos x$
$=-4\cos^3 x \sin x$.
Conclusion: The derivative of cos^4 x is -4cos^3(x) sinx and this is obtained by the chain rule and the power rule of derivatives.
In a similar way, one can obtain the derivative of \cos^n x, which is given below:
$\dfrac{d}{dx}(\cos^n x)=-n\cos^{n-1}x \sin x$.
For example,
- The derivative of $\cos^2x$ is $-2\cos x\sin x$.
- The derivative of $\cos^3x$ is $-2\cos^2 x\sin x$.
- The derivative of $\cos^5x$ is $-5\cos^4 x\sin x$.
Also Read:
FAQs
Q1: What is the derivative of cos^4x?
Answer: The derivative of cos4x is equal to -4cos3x sinx.