1-cosx Identity, Proof | 1-cosx Formula [in terms of sin]

The 1-cosx identity is given by 1-cosx= 2sin²(x/2). 1 minus cosx is a trigonometric expression and its formula is given below:

$1-\cos x =2 \sin^2 (\frac{x}{2})$.

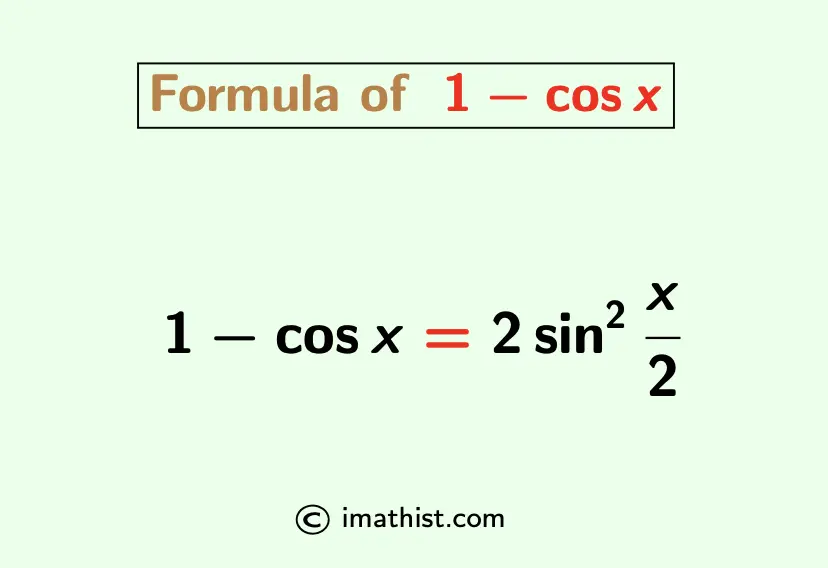
Let us now find the formula of 1-cosx in terms of sin.

1-cosx Formula in Terms of Sin

Answer: 1-cosx formula in terms of sin is equal to 1-cosx= 2sin²(x/2).

Explanation:

The given expression is

1- cosx

= 1-cos $\big(2 \cdot \dfrac{x}{2} \big)$ as we can write x=2⋅x/2.

= $1- \big[\cos^2 \dfrac{x}{2} – \sin^2 \dfrac{x}{2} \big]$, obtained by using the formula: cos2A= cos²A -sin²A.

= $1- \cos^2 \dfrac{x}{2} + \sin^2 \dfrac{x}{2}$

= $\sin^2 \dfrac{x}{2} + \sin^2 \dfrac{x}{2}$, by the identity 1-cos²A=sin²A.

= $2\sin^2 \dfrac{x}{2}$

Therefore, $1-\cos x=2\sin^2 \dfrac{x}{2}$.

So the formula of 1-cosx in terms of sin is given by 1-cosx= 2sin²(x/2).

Also Read: Sin3x formula in terms of sinx

Cos3x formula in terms of cosx

Solved Examples

Example 1: Find the value of 1-cos120°.

Solution:

By the above formula,

1-cos120°

= 2sin²(120/2)°

= 2sin²60°

= 2 × $(\frac{\sqrt{3}}{2})^2$ as the value of sin60 is √3/2.

= (2 ×3)/4

= 3/2.

So the value of 1-cos120° is equal to 3/2.

Read Also: cot(a+b)cot(a-b) Formula

Find values of sin18, cos18

FAQs