Maclaurin series expansion of e^x | Taylor series of e^x

The Maclaurin series expansion of e^x or the Taylor series expansion of e^x at x=0 is given by the following summation:

e^x = $\sum_{n=0}^\infty \dfrac{x^n}{n!}$

= $1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\cdots$.

In this post, we will learn how to find the series expansion of e^x.

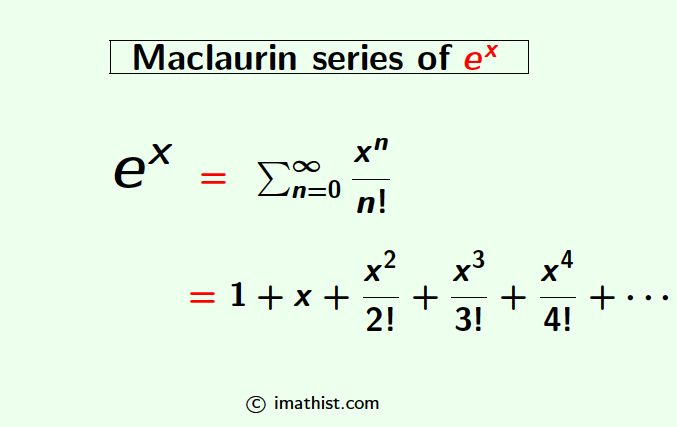
Taylor Series Expansion of e^x at x=0

The Maclaurin series expansion of a function f(x), that is, the Taylor series of f(x) at x=0 is given as follows:

$f(x)=\sum_{n=0}^\infty \dfrac{f^{(n)}(0)}{n!} x^n$ …(∗)

where f⁽ⁿ⁾ denotes the n-th derivative of f(x). The 0-th derivative of f(x) is equal to f(0).

Put f(x)=e^x.

As the derivative of e^x is e^x itself, we have:

f(0) = e⁰ = 1.

f$’$(x) = e^x ⇒ f$’$(0) = e⁰ = 1

f$^{”}$(x) = e^x ⇒ f$^{”}$(0) = e⁰ = 1

f⁽³⁾(x) = e^x ⇒ f⁽³⁾(0) = e⁰ = 1

f⁽⁴⁾(x) = e^x ⇒ f⁽⁴⁾(0) = e⁰ = 1

ans so on.

Substituting the above values in (∗) , the Maclaurin series expansion for f(x)=e^x is equal to

$f(x)=f(0)+xf'(0)+\dfrac{x^2}{2!}f^{”}(0)$ $+\dfrac{x^3}{3!}f^{(3)}(0)$ $+\dfrac{x^4}{4!}f^{(4)}(0)+\cdots$

⇒ $e^x$ $=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\dfrac{x^4}{4!}+\cdots$.

In sigma notation, the Maclaurin series expansion of e^x will be equal to

e^x = $\sum_{n=0}^\infty \dfrac{x^n}{n!}$.

Note that the above series for e^x converges for all real values. So the radius of converges of e^x series expansion is the interval (-∞, ∞).

Also Read: 

Maclaurin series expansion of sinx

Maclaurin series expansion of cosx

FAQs