The integration of root x + 1/root x is equal to 2/3 x3/2+2√x+C where C is an integral constant. In this post, we will learn how to integrate √x+1/√x.
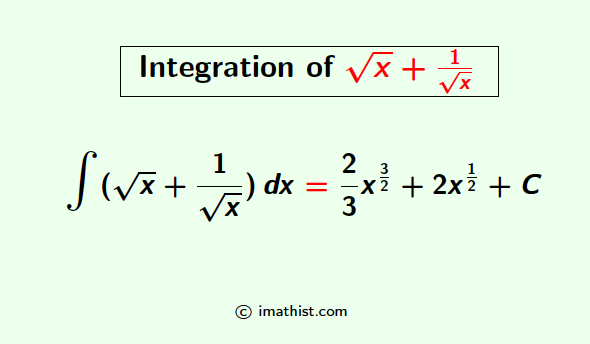
Integral of √x+1/√x
Question: Find the integral $\int (\sqrt{x}+\dfrac{1}{\sqrt{x}})\ dx$
Answer:
$\int (\sqrt{x}+\dfrac{1}{\sqrt{x}})\ dx$ = $\int \sqrt{x}\ dx$ + $\int \dfrac{1}{\sqrt{x}}\ dx$ by the sum rule of integration.
= ∫ x1/2 dx + $\int \dfrac{1}{x^{1/2}}\ dx$
= ∫ x1/2 dx + ∫ x-1/2 dx
= $\dfrac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}$ + $\dfrac{x^{-\frac{1}{2}+1}}{-\frac{1}{2}+1}$ using the power rule of integration: $\int x^n dx =\dfrac{x^{n+1}}{n+1}$
= $\dfrac{x^{3/2}}{3/2}$ + $\dfrac{x^{1/2}}{1/2}$ + C where C is an integration constant.
= $\dfrac{2}{3} x^{3/2}$ $+2 \sqrt{x}$ + C
= $\dfrac{2}{3} x\sqrt{x}$ $+2 \sqrt{x}$ + C as we have $x^{3/2}=x\sqrt{x}$ by the power rule of indices.
So the integral of √x+1/√x is equal to $\dfrac{2}{3} x\sqrt{x}$ $+2 \sqrt{x}$ + C where C is an integration constant.
ALSO READ:
FAQ
Q1: What is the integration of √x+1/√x?
Answer: The integration of √x+1/√x is equal to ∫(√x+1/√x)dx = 2/3 x√x + 2√x + C.