Integral of 1/2x (1 by 2x) | How to Integrate 1/2x

The integral of 1/2x (1 by 2x) is equal to 1/2 ln|x|+C where C denotes an integration constant. Here we learn how to integrate 1/2x. The integration of 1/2x formula is given by

$\int \dfrac{1}{2x} dx=\dfrac{1}{2}\ln |x|+C$.

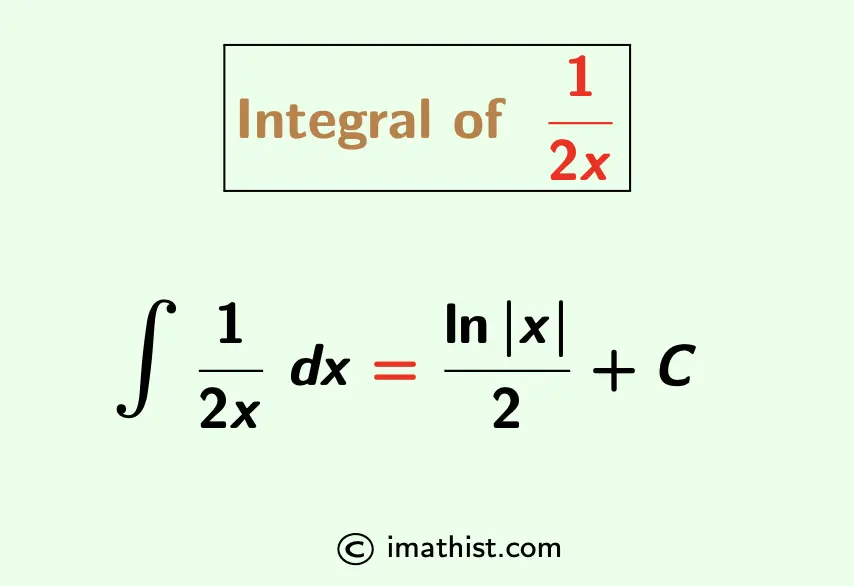
Integration of 1/2x

Answer: The integration of 1/2x is 1/2 ln|x|+C.

Explanation:

We need to find the integral

$\int \dfrac{1}{2x} \ dx$.

Let us put ln x = t.

Differentiating, $\dfrac{dx}{x}$ = dt.

Thus, $\int \dfrac{1}{2x} \ dx$

= $\dfrac{1}{2} \int \dfrac{dx}{x}$ as 1/2 is a constant.

= $\dfrac{1}{2} \int dt$

= $\dfrac{1}{2} t +C$

= $\dfrac{1}{2} \ln |x| +C$ as ln is defined for positive values only.

That is, $\int \dfrac{1}{2x} \ dx$ = $\dfrac{1}{2} \ln |x| +C$.

So the integration of 1/2x is equal to 1/2 ln|x|+C where C denotes an arbitrary integral constant.

More Integrals:

Integral of ln(x) | Integral of ln2x

Integration of square root of cotx

Integartion of tanx

FAQs