How to Integrate Root (1-x^2)?

The integral of $\sqrt{1-x^2}$ is equal to $\dfrac{x}{2} \sqrt{1-x^2}$ $+\dfrac{1}{2}$ sin^-1 x+C. Here we will learn how to integrate square root of 1-x².

The integral formula of root 1-x^2 is provided below:
$\int \sqrt{1-x^2} dx$ $=\dfrac{x}{2} \sqrt{1-x^2}$ $+\dfrac{1}{2}$ sin^-1 x+C.

Table of Contents

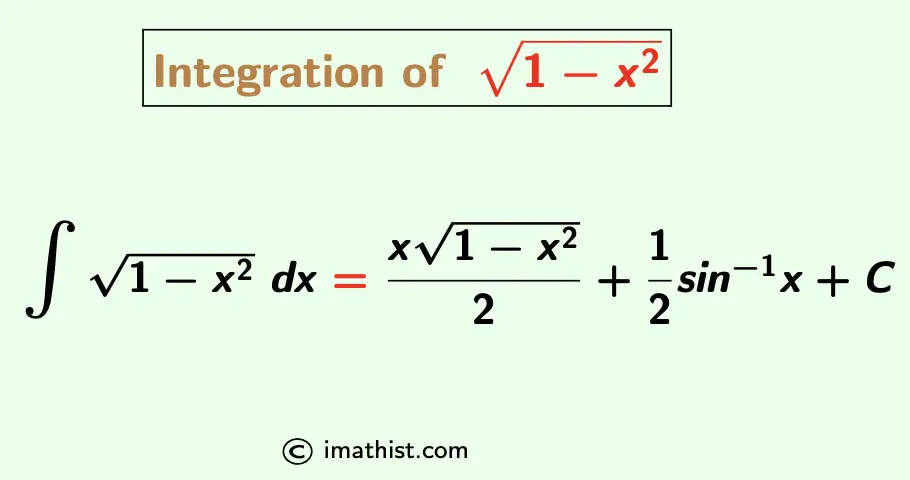
Integration of $\sqrt{1-x^2}$

Question: How to Integrate Root (1-x^2)?

That is, find $\int \sqrt{1-x^2} dx$.

Solution:

Let x = sint.

So dx = cost dt

Also, we have

sin2t = 2sint cost = 2sint $\sqrt{1-\sin^2t}$ = 2x$\sqrt{1-x^2}$ …(∗)
t = sin^-1x …(∗∗)

Now, $\int \sqrt{1-x^2} dx$

= $\int \sqrt{1-\sin^2t} \cos t \,dt$

= $\int \cos^2 t \, dt$ as we know cos²θ=1-sin²θ

= $\dfrac{1}{2}\int 2\cos^2 t \,dt$

= $\dfrac{1}{2}\int (1+\cos 2t) dt$ as 1+cos2θ = 2cos²θ.

= $\dfrac{1}{2} \big(t+\dfrac{\sin 2t}{2} \big)$+C

= $\dfrac{1}{2} \big(\sin^{-1}x+\dfrac{2x\sqrt{1-x^2}}{2} \big)$+C, using Equations (∗) and (∗∗).

= $\dfrac{x}{2} \sqrt{1-x^2}$ $+\dfrac{1}{2}$sin^-1 x+C.

So the integration of $\sqrt{1-x^2}$ is equal to $\int \sqrt{1-x^2} dx$ $=\dfrac{x}{2} \sqrt{1-x^2}$ $+\dfrac{1}{2}$ sin^-1 x+C, where C is an integration constant.

Have You Read These?

Integration of $\sqrt{a^2+x^2}$

Integration of $\sqrt{a^2-x^2}$

Integration of 1/(1+x²)