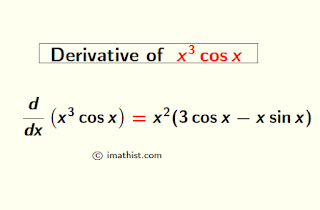Derivative of x^3 cosx | x^3 cos x-2^x tanx Derivative

The derivative of x³ cosx is equal to 3x²cosx – x³sinx. The function x³cosx is the product of two functions x cube and cosx. In this post, we will find the derivative of x³cosx.

What is the Derivative of x³cosx?

Answer: The derivative of x3cosx is equal to 3x²cosx-x³sinx.

Explanation:

We will use the product rule of derivatives here. The rule tells us that if f(x) is a function of two functions g(x) and h(x), that is,

f(x) = g(x) h(x),

then the derivative of f(x) with respect to x is given as follows:

$\dfrac{df}{dx}=g \cdot \dfrac{dh}{dx}+\dfrac{dg}{dx} \cdot h$ $\cdots (*)$

We will follow the below steps to find the derivative of $x^3\cos x$ by the product rule of derivatives.

Step 1: As $f(x)=x^3\cos x$, we have $g(x)=x^3$ and $h(x)=\cos x$.

Step 2: See that

• $\dfrac{d}{dx}(g(x))=\dfrac{d}{dx}(x^3)=3x^2$ by the power rule of derivatives.
• $\dfrac{d}{dx}(h(x))=\dfrac{d}{dx}(\cos x)=-\sin x$.

Step 3: Now applying the above product rule (*) of derivatives, we obtain that

$\dfrac{d}{dx}(x^3\cos x)$ $=x^3 \dfrac{d}{dx}(\cos x) +\cos x \dfrac{d}{dx}(x^3)$

$=x^3\cdot (-\sin x) + \cos x \cdot 3x^2$

$=3x^2\cos x -x^3\sin x$

$=x^2(3\cos x -x\sin x)$

Thus, the derivative of x3cosx by the product rule of derivatives is equal to x²(3cosx-x sinx).

Also Read:

Derivative of 1/root(x)

Derivative of x

Derivative of x²

Derivative of cos² x

Derivative of sin² x

Question Answer on Derivative of x³cosx

Question 1: Find the derivative of $x^3\cos x -2^x \tan x$

Answer:

From above we have the derivative of $x^3\cos x$ which is $\dfrac{d}{dx}(x^3\cos x)$$=x^2(3\cos x -x\sin x)$. Now we will evaluate the derivative of $2^x \tan x$ by the product rule.

$\dfrac{d}{dx}(2^x \tan x)$ $=2^x \dfrac{d}{dx}(\tan x)$ $+\tan x \dfrac{d}{dx}(2^x)$

$=2^x \sec^2 x+\tan x \cdot 2^x \log 2$

$=2^x(\sec^2 x +\log 2 \tan x)$

Now, by the sum/difference rule of derivative, we obtain the derivative of x³ cosx-2^xtanx which is equal to

$\dfrac{d}{dx}(x^3\cos x -2^x \tan x)$

$=\dfrac{d}{dx}(x^3\cos x) -\dfrac{d}{dx}(2^x \tan x)$

$=x^2(3\cos x -x\sin x)$ $-2^x(\sec^2 x +\log 2 \tan x)$

FAQs