Derivative of sinx with respect to cosx

The derivative of sinx with respect to cosx is denoted by d/dcosx (sinx), and it is equal to -cotx. That is,

$\dfrac{d}{d \cos x}(\sin x)=-\cot x$.

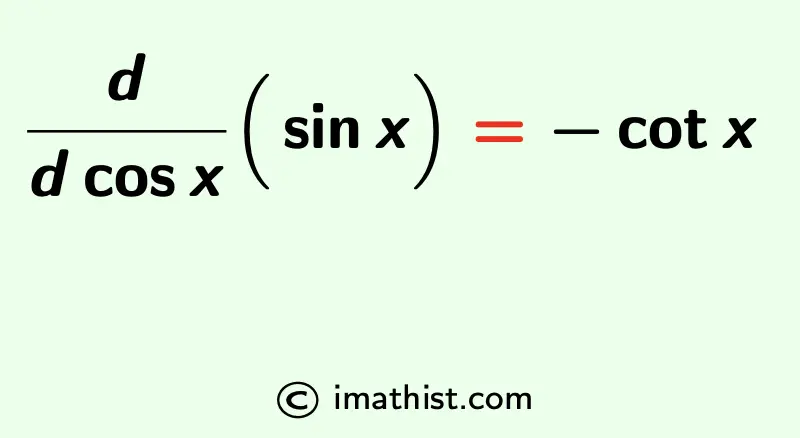
Let us now learn how to differentiate sin x with respect to cos x.

Derivative of sinx w.r.t cosx

Question: Find the derivative of sinx w.r.t cosx, that is,

Find $\dfrac{d}{d \cos x}(\sin x)$.

Answer:

Let u=sinx and v=cosx.

So we need to find $\dfrac{du}{dv}$.

Differentiating u and v with respect to x, we get that

$\dfrac{du}{dx}=\cos x$ and $\dfrac{dv}{dx}=-\sin x$

Therefore,

$\dfrac{du}{dv} = \dfrac{\frac{du}{dx}}{\frac{dv}{dx}}$

⇒ $\dfrac{du}{dv}$ = $\dfrac{\cos x}{-\sin x}$

⇒ $\dfrac{du}{dv}$ = – cotx.

So the derivative of sinx with respect to cosx is equal to -cotx.

More Derivatives: Derivative of natural log of x

Derivative of x^lnx

Derivative of e^sinx | Derivative of e^cosx

FAQs