Derivative of e^cosx by First Principle

The derivative of e^cosx (e to the power cosx) is equal to -sinx e^cosx. In this post, we will find the derivative of e^cosx by first principle.

The derivative formula of e^cosx is given below:

$\dfrac{d}{dx}$(e^cosx) = -sinx e^cosx.

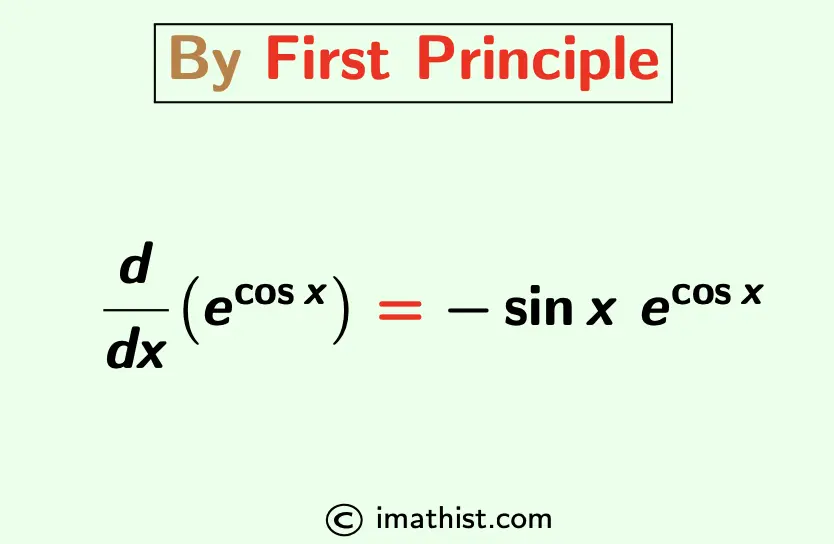
Derivative of e^cosx Using First Principle

By first principle, the derivative of a function f(x) using the first principle is given by the following limit formula:

$\dfrac{d}{dx}$ ( f(x) ) = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$.

Put f(x) = e^cosx.

So $\dfrac{d}{dx}$ ( e^cosx ) = lim_h→0 $\dfrac{e^{\cos(x+h)} – e^{\cos x}}{h}$

= lim_h→0 $\dfrac{e^{\cos x}(e^{\cos(x+h)-\cos x} -1)}{h}$

= e^cosx lim_h→0 $\dfrac{e^{\cos(x+h)-\cos x} -1}{h}$

= e^cosx lim_h→0 $\dfrac{e^{\cos(x+h)-\cos x} -1}{\cos(x+h)-\cos x}$ × lim_h→0 $\dfrac{\cos(x+h)-\cos x}{h}$

[Let z=cos(x+h) -cosx. Then z→0 as h→0]

= e^cosx lim_z→0 $\dfrac{e^z-1}{z}$ × lim_h→0 $\dfrac{-2\sin(x+\frac{h}{2})\sin \frac{h}{2}}{h}$, using the formula cosa – cosb= – 2 sin(a+b)/2 sin(a-b)/2.

= e^cosx × 1 × lim_h→0 $- \sin(x+\frac{h}{2})$ × lim_h→0 $\dfrac{\sin \frac{h}{2}}{\frac{h}{2}}$ using the limit formula lim_t→0(e^t-1)/t =1.

= – e^cosx $\sin(x+\frac{0}{2})$ × lim_u→0 sinu/u where u=h/2.

= – sinx e^cosx as the limit of sinx/x is 1 when x→0.

So the derivative of e^cosx is equal to -sinx e^cosx, and this is obtained by the first principle of derivatives.

More Derivatives: Derivative of e^sinx by first principle

Derivative of root sinx

Derivative of root cosx

Derivative of log(sin x)

FAQs