Integration of x/(1+x^2) | Integral of x/(1+x^2)

The integration of x/(1+x^2), that is, the integral of x divided by 1+x² is equal to 1/2 ln(1+x²) + C, where C is a constant. Here ln denotes the natural logarithm. In this post, we will learn how to integrate x divided by 1+x^2.

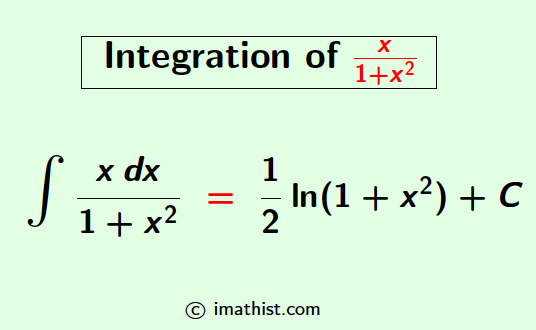
Let’s find the integral:

$\int \dfrac{x}{1+x^2} dx$.

To find the above integral, we will use the following integration formula:

$\color{blue}{\int \dfrac{dt}{t}=\ln |t|+C}$ …(I)

How to Integrate x/(1+x²)

Question: Find the integral of x/(1+x²), that is, find

$\int \dfrac{x}{1+x^2} dx$

Solution:

To integrate x/(1+x²), let us put $\color{blue}{z=1+x^2}$.

Differentiating both sides with respect to x, we get that

$\dfrac{dz}{dx}$ = 2x

∴ xdx = dz/2

Thu, substituting these values we get that

$\int \dfrac{x}{1+x^2} dx$ = $\int \dfrac{1}{z} \dfrac{dz}{2}$

= $\dfrac{1}{2} \int \dfrac{dz}{z}$

= $\dfrac{1}{2} \ln|z|+C$ by the above integration formula.

= $\dfrac{1}{2} \ln(1+x^2)+C$, putting back the value of z=1+x² and noting z is always positive.

So the integration of x divided by 1+x^2 is equal to 1/2 ln(1+x²) +C and this is obtained by the substitution method of integration. Here C is an integration constant.

Have You Read These?

Integration of Root 1+sin2x

Integration of Root x

Integration of Cube Root x

FAQs