Find the Derivative of arc(cotx) | Differentiate cot^-1x

The derivative of arc(cotx) is equal to -1/(1+x²). In this post, we will learn how to differentiate cot inverse x.

The derivative formula of cot^-1x is given by d/dx (cot^-1x) = -1/(1+x²).

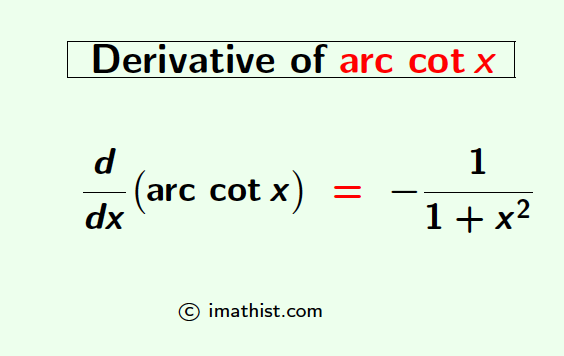
What is the derivative of arc cotx?

Answer: The derivative of arccotx is -1/(1+x²).

Solution:

Let y = arc cotx …(∗)

As we need to find the derivative of arccot x, so we have to calculate dy/dx. From (∗) we get that

y = cot^-1x

⇒ coty = x …(∗∗)

We now differentiate both sides of (∗∗) with respect to x. So we obatin that

$\dfrac{d}{dx}$(coty) = $\dfrac{dx}{dx}$

⇒ $- \text{cosec}^2 y \dfrac{dy}{dx}$ =1

⇒ $\dfrac{dy}{dx}$ = $-\dfrac{1}{\text{cosec}^2 y}$

Now, using the trigonometric formula cosec²y = 1+cot²y, we deduce that

$\dfrac{dy}{dx}$ = – $\dfrac{1}{1+\cot^2 y}$

So $\dfrac{dy}{dx}$ = – $\dfrac{1}{1+x^2}$ as coty = x by (∗∗)

Thus, the derivative of arc cotx, that is, the differentiation of cot inverse x is equal to – 1/(1+x²).

Differentiation of cot inverse x

To find the derivative of cot inverse x, we will use the differentiation of tan inverse x. We know that

tan^-1x + cot^-1x = π/2

Differentiating both sides of the above equation, we get that

$\dfrac{d}{dx}$(tan^-1x) + $\dfrac{d}{dx}$(cot^-1x) = 0 as we know that the derivative of a constant is zero and π/2 here is a constant.

⇒ 1/(1+x²) + $\dfrac{d}{dx}$(cot^-1x) =0

⇒ $\dfrac{d}{dx}$(cot^-1x) = -1/(1+x²).

Thus, we have proven that the derivative of arccot x is -1/(1+x²).

Question Answer

Q1: What is the derivative of arc cot 2x?

Answer:

Note that arc(cot2x) = cot^-1(2x).

Put t=2x.

So dt/dx=2.

Now, by the chain rule of differentiation, the derivative of arc cot(2x) will be equal to

$\dfrac{d}{dx}(\text{arc} \cot 2x)$ $=\dfrac{d}{dt}(\text{arc} \cot t) \times \dfrac{dt}{dx}$ ⇒ $\dfrac{d}{dx}(\text{arc} \cot 2x)$ $=\dfrac{-1}{1+t^2} \times 2$ as t=2x. ⇒ $\dfrac{d}{dx}(\text{arc} \cot 2x)$ $=- \dfrac{2}{1+4x^2}$.

So the derivative of cot inverse 2x is equal to -2/(1+4x²).

ALSO READ

• Derivative of root tanx
• Derivative of 1/sinx
• Derivative of 1/cosx

FAQs