Derivative of x^e (x to the power e)

The derivative of x^e (x to the power e) is equal to ex^e-1. Here we will learn to differentiate x^e with respect to x. The derivative of x^e is denoted by d/dx (x^e) or (x^e)’. Its formula is given by

$\dfrac{d}{dx}(x^e)=ex^{e-1}$.

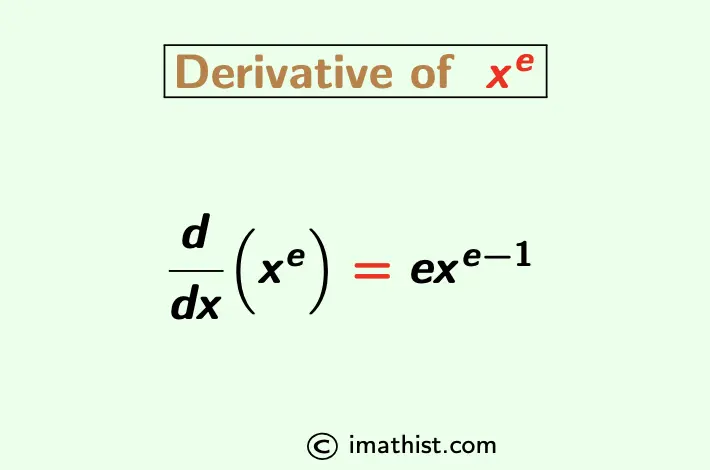
Derivative of x to the power e

Question: Find the derivative of x^e, that is, Find

$\dfrac{d}{dx}(x^e)$.

Answer:

As the number e is an irrational number, so it is a constant, whose value lies between 2 and 3.

Thus, we can apply the power rule of derivatives: $\dfrac{d}{dx}$(xⁿ) = nx^n-1 in order to get the derivative of x^e.

Applying this formula, we obtain that

$\dfrac{d}{dx}$(x^e) = ex^e-1.

So the derivative of x^e is equal to ex^e-1, and this is obtained by the power rule of derivatives.

Question-Answer

Question: Find the derivative of $x^{e^2}$ (x to the power e2).

Answer:

As e² is a constant, by the power rule of derivatives,

$\dfrac{d}{dx}(x^{e^2})=e^2 x^{e^2-1}$.

So the derivative of x to the power e^2 is equal to $e^2 x^{e^2-1}$.

More Derivatives:

What is the Derivative of e^1/x?

What is the Derivative of π?

Find the derivative of 2^x

Find the derivative of e²

FAQs