Integration of log(sin x) from 0 to pi/2

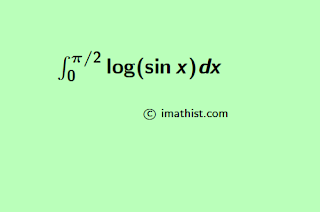
The integration of log(sin x) from 0 to pi/2 is -π/2 log2. In this section, we will find the integral of log sinx from 0 to pi/2. The following property will be used to calculate the integral.

$\int_0^af(x)dx=\int_0^af(a-x)dx$ …(i)

Integral of log(sin x) from 0 to pi/2

Question:

Show that $\int_0^{\frac{\pi}{2}} \log \sin x dx = – \frac{\pi}{2} \log 2$

Solution:

Let I = $\int_0^{\frac{\pi}{2}}$ log sinx dx …(ii)

Using the above property (i), we have

I = $\int_0^{\frac{\pi}{2}}$ log sinx dx = $\int_0^{\frac{\pi}{2}}$ log sin($\frac{\pi}{2}$-x)dx.

By the fact $\sin(\frac{\pi}{2}-x)=\cos x$ we get that

$I=\int_0^{\frac{\pi}{2}}\log \cos x dx$ ...(iii)

Adding (ii) and (iii), we obtain that

2I = $\int_0^{\frac{\pi}{2}}$ (log sin x+log cos x)dx

⇒ 2I = $\int_0^{\frac{\pi}{2}}$ log(sin x cos x)dx as log(a) + log(b)=log(ab)

⇒ 2I = $\int_0^{\frac{\pi}{2}} \log(\frac{\sin 2x}{2})dx$ as sin(2x)=2sin x cos x

⇒ 2I = $\int_0^{\frac{\pi}{2}}(\log \sin 2x-\log 2)dx$ as log(a) – log(b)=log(a/b)

⇒ 2I = $\int_0^{\frac{\pi}{2}}\log \sin 2x dx$ $- \int_0^{\frac{\pi}{2}} \log 2dx$

⇒ 2I = $\int_0^{\frac{\pi}{2}}\log \sin 2x dx-\frac{\pi}{2}\log 2$ …(iv)

Let $I_1=\int_0^{\frac{\pi}{2}}\log \sin 2xdx$

Put t=2x.

Therefore, dt=2 dx. Thus dx=dt/2.

Note that t=π when x=π/2 and t=0 when x=0.

So $I_1=\frac{1}{2}\int_0^\pi\log(\sin t) dt$ …(v)

Property: $\int_0^{2a}f(x)dx=2\int_0^a f(a-x)dx$ when $f(2a-x)=f(x)$

Observe that we have log(sin t)=log sin(π-t).

Thus, by the above property 

$I_1=\frac{1}{2} \cdot 2 \int_0^{\frac{\pi}{2}} \log(\sin t) dt$

$=\int_0^{\frac{\pi}{2}} \log(\sin t) dt=I$

As $I_1=I$ we deduce from (iv) and (v) that

$2I =I-(\frac{\pi}{2})\log 2$

$\Rightarrow I=-\frac{\pi}{2} \log 2$

So we finally get that

$\int_0^{\frac{\pi}{2}} \log \sin x=-\frac{\pi}{2}\log 2$

Also Read:

Derivative of log(sinx)

Derivative of log(cosx)

Derivative of (sinx)^logx

Derivative of root(x)+1/root(x)