Find the Derivative of sin(xy)

The derivative of sin(xy) is equal to (y+x dy/dx) cos(xy), and this is the derivative of sin(xy) with respect to x.

The derivative of sin(xy) formula is given below:

$\dfrac{d}{dx}(\sin xy)=(y+x\dfrac{dy}{dx})\cos xy$.

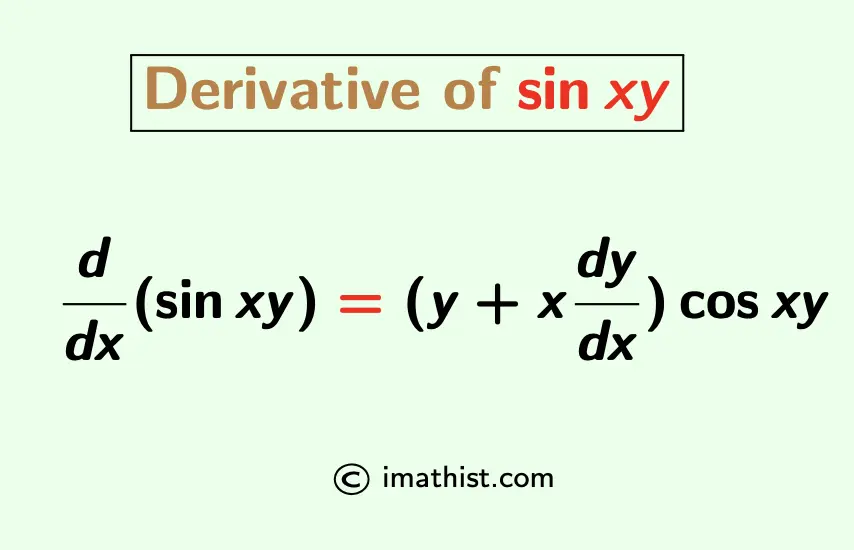
Differentiate sin(xy) with respect to x

Answer: The derivative of sin(xy) with respect to x is equal to (y+x dy/dx) cos(xy).

Explanation:

Let us use the chain rule of derivatives in order to differentiate sin(xy).

Put z=xy.

Differentiating with respect to x,

$\dfrac{dz}{dx}=y+x\dfrac{dy}{dx}$ by the product rule.

Now, by the chain rule,

$\dfrac{d}{dx}(\sin xy)= \dfrac{d}{dx}(\sin z)$

= $\dfrac{d}{dz}(\sin z) \times \dfrac{dz}{dx}$, by the chain rule.

= $\cos z \times (y+x\dfrac{dy}{dx})$ as the derivative of sinx is cosx.

= $\cos(xy) (y+x\dfrac{dy}{dx})$ as z=xy.

So the derivative of sin(xy) is equal to (y+x dy/dx) cos(xy), and this is obtained by the chain and product rule of derivatives.

FAQs